Drift AMM
Introduction
Drift uses a backstop AMM as a source of guaranteed constant liquidity for the exchange, providing constant liquidity to be taken against asynchronously.
Drift's v1 featured a Dynamic AMM (DAMM) which was an iteration on top of Perpetual Protocol's innovation - the virtual AMM (vAMM), except with configurable parameters, namely:
-
Peg: a price multiplier
-
K: liquidity depth
-
Fee Pool: comprised of taker fee amounts (multiple methods for fee discounts to be implemented in the future)
-
Fee Tranches: percentage allocations from the fee pool to be distributed amongst the following operations:
-
Adjusting Peg (alternatively, "repeg")
-
kadjustments -
(Capped) funding payments
-
You can read more about Drift's v1 DAMM design here.
Drift v2 AMM
Drift’s v2 AMM is still a vAMM using a constant product curve but now includes external Liquidity Providers (LPs), a concentration factor, and dynamic spread/peg that programmatically update prior to filling trades.
The mechanics behind the dynamic spread and peg are:
-
Inventory adjusted spreads
-
Oracle live pricing/volatility
Inventory Adjusted Spreads
In a typical constant product AMM, the AMM quotes the same price for buys/sells and charges a flat fee.
To implicitly utilise a dynamic fee, Drift v2's AMM quotes different prices for buys and sells. The offset from the mid-price is dynamic based on the current inventory.
To do so, there will be 3 points tracked on the constant product curve: the bid price and ask price, and a point between the reservation price.
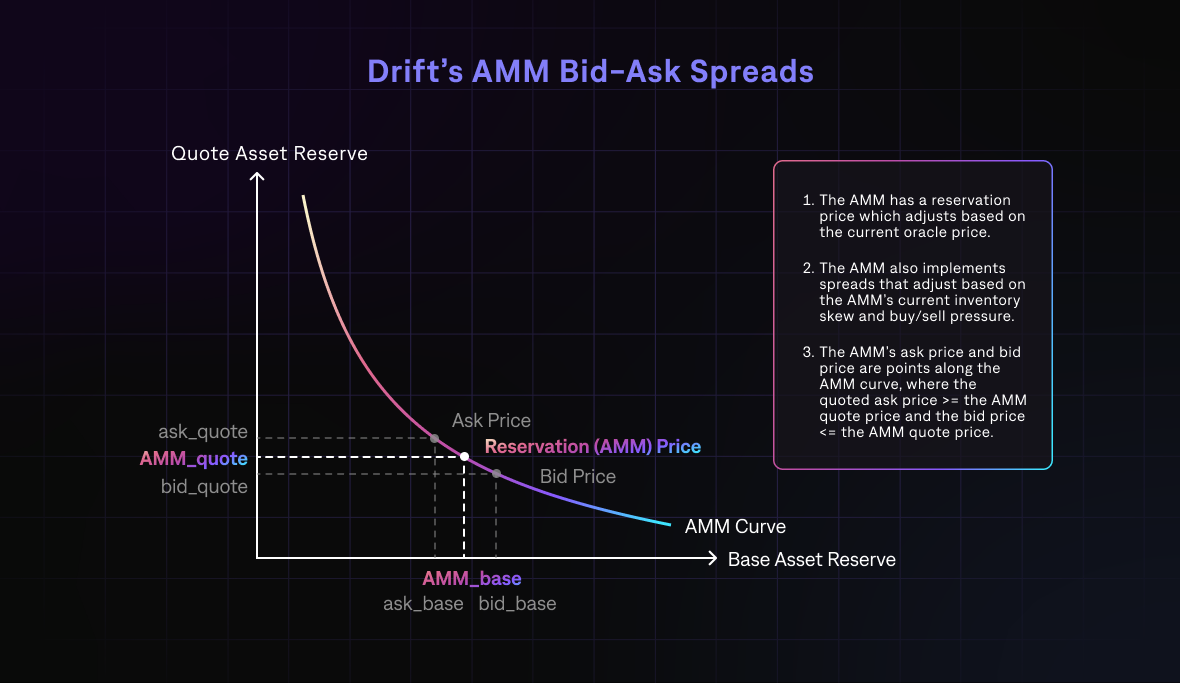
Base long spread and short spread are currently set as:
bid/ask price = reservation price ± base_spread + f(inventory, balance, ...)
The long and short spread can be asymmetric due to changes in the underlying inventory skew and market buy/sell pressure. Ultimately, the ask - bid can never exceed the max spread (percentage calculated using the current valid oracle price).
The bid/ask points on the curve are calculated as follows (exact efficient integer math method calculated on contract):
bid_quote_reserve = quote_reserve - (quote_reserve / (100%/short_spread)) ask_quote_reserve = quote_reserve + (quote_reserve / (100%/long_spread))
The quote_reserve is defined as the total AMM reserves of the quote asset. Then using the same k to back out the base_reserve for the bid/ask curves as well.
Oracle Live Pricing
The AMM's reservation price gets updated regularly through Drift's live oracle-based pricing.
This pricing mechanism updates an asset's mark price towards its oracle price, achieving:
-
more accurate pricing; and
-
better entries and exits closer to oracle price.
The mark price is updated each time the oracle updates its price and when the contract is interacted with.
Oracle Live Pricing Sequence
Every time a trader wants to fill against the AMM, the AMM will be updated in the same slot with a valid oracle price (see Oracles).
The sequence is:
-
The AMM checks the oracle price
-
The AMM move its peg toward the oracle price
-
The AMM sets its bid/ask spread versus its reservation price
-
The order will fill according to the bid/ask price if the order has lived longer than the minimum duration for AMM fills (10 slots)
The overall spread will increase if the AMM is heavily levered or in debt. The oracle price and reservation price are always within this spread. Effective leverage is a function of many market stats, including Inventory P&L and collateral within the fee pool in the terminal state.
The reservation (AMM) price is the .